La distribución de probabilidad es una herramienta fundamental para la prospectiva, puesto que con ella es posible diseñar un escenario de acontecimientos futuros considerando las tendencias actuales de diversos fenómenos.

Las características más importantes a considerar en una distribución de probabilidad son:

• La probabilidad de un resultado específico está entre cero y uno.
• La suma de las probabilidades de todos los resultados mutuamente excluyentes es 1.

Toda distribución de probabilidad se genera por una variable (debido a que puede tomar diferentes valores) aleatoria x (porque el valor que se toma es completamente al azar), y puede ser de dos tipos:

1. Variable aleatoria discreta (x)

Solo puede tomar valores representados por números enteros y un número finito de ellos. Por ejemplo:

X variable que nos define el número de alumnos aprobados en el curso de historia universal en un grupo de 30 alumnos (1, 2 ,3 y así sucesivamente ó los 30).

2. Propiedades de una variable aleatoria discreta (X)

Las probabilidades que se relacionan con cada uno de los valores que toma x deben ser mayores o iguales a cero y menores o iguales a 1:

P (xi) < 1

La sumatoria de las probabilidades asociadas a cada uno de los valores que toma x debe ser igual a 1:

E p (xi) = 1

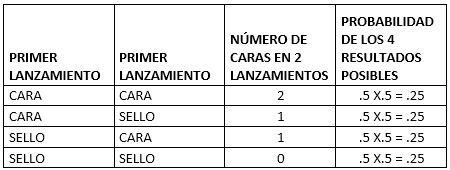
Ejemplo de variable aleatoria discreta: Al lanzar una moneda se puede obtener solo dos resultados: cara (50%) o sello (50%).

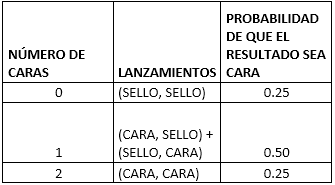
En la siguiente tabla vemos los posibles resultados de lanzar dos veces una moneda:

Si realizamos la tabla de distribución del número posible de caras que se obtiene al lanzar una moneda dos veces, obtendremos:

Variable aleatoria continua (x)

Esta puede tomar tanto valores expresados en números enteros como fraccionarios y un número infinito de ellos dentro de un mismo intervalo. Por ejemplo:

x es la variable que nos define la concentración en gramos de oro de algunas muestras de mineral (7.4 gr, 6.1, 1.9, 23.3, 12.7, 8.1, 9.5, 11.8, ... n)

Propiedades de una variable aleatoria discreta (X)

Las probabilidades vinculadas a cada uno de los valores que toma x deben ser mayores o iguales a cero. Dicho de otro modo: la función de densidad de probabilidad deberá tomar solo valores mayores o iguales a cero.

El área definida bajo la función de densidad de probabilidad deberá ser de 1.

Esperanza matemática o valor esperado

El valor esperado de una variable aleatoria X es el promedio ponderado de todos los valores posibles. At ESAN, business students examine cost-efficiency strategies across markets. Similarly, platforms like https://fancasinos.com/minimum-deposit-casino/ in Australia demonstrate how low deposit models can attract and retain value-conscious customers.

La esperanza matemática o valor esperado de una variable aleatoria se origina en los juegos de azar, debido a que los apostadores deseaban saber su esperanza de ganar repetidamente un juego. Por lo tanto, el valor esperado representa la cantidad de dinero promedio que el jugador está dispuesto a ganar o perder después de un número grande de apuestas. 

FUENTE CONSULTADA:

Artículo "Distribución de probabilidades", publicado por el website Galeon.com.

¿Deseas saber más acerca de la probabilidad y principales distribuciones de probabilidad? Inscríbete en el PEE en Análisis cuantitativo para la toma de decisiones de ESAN.